Input
Input data should be formatted as a data frame, with one row for each observation, and one column for each feature. The first column should contain the true class labels. Factor features (ex: gender, site, etc.) should be coded as multiple numeric “dummy” features (see ?model.matrix for how to automatically generate these in R).
An example dataset (derived from a bit of the ADHD200 sample is included:
set.seed(12345)
library(e1071)
library(mRFE)
data(input)
dim(input)
#> [1] 208 547
input[1:5,1:5]
#> DX2 Full4.IQ Age bankssts_SurfArea caudalanteriorcingulate_SurfArea
#> 1000804 TD 109 7.29 1041 647
#> 1023964 ADHD 123 8.29 1093 563
#> 1057962 ADHD 129 8.78 1502 738
#> 1099481 ADHD 116 8.04 826 475
#> 1127915 TD 124 12.44 1185 846There are 208 observations (individual subjects), and 546 features. The first column (DX2) contains the class labels (TD: typically-developing control, ADHD: attention deficit hyperactivity disorder).
svmRFE
To perform the feature ranking, use the svmRFE function:
res <- svmRFE(input, k = 10, halve.above = 100)Here we’ve indicated that we want k=10 for the k-fold cross validation as the “multiple” part of mSVM-RFE. To use standard SVM-RFE, you can use k=1. Also notice the halve.above parameter. This allows you to cut the features in half each round, instead of one by one. This is very useful for data sets with many features. Here we’ve set halve.above=100, so the features will be cut in half each round until there are fewer than 100 remaining. The output is a vector of feature indices, now ordered from most to least “useful”.
Note that because of the randomness of the CV draws, features with close ranking scores, and the possible inclusion of useless features, these rankings can change some run to run. However, your output for this demo should be identical because we’ve all reset the random seed to the same value.
Estimating generalization error
When exploring machine learning options, it is often useful to estimate generalization error and use this as a benchmark. However, it is important to remember that the feature selection step must be repeated from scratch on each training set in whatever cross validation or similar resampling scheme chosen. When feature selection is performed on a data set with many features, it will pick some truly useful features that will generalize, but it will also likely pick some useless features that, by mere chance, happened to align closely with the class labels of the training set. While including these features will give (spuriously) good performance if the error is estimated from this training set itself, the estimated performance will decrease to its true value when the classifier is applied to a true test set where these features are useless. Guyon et al. actually made this mistake in the example demos in their original SVM-RFE paper. This issue is outlined very nicely in “Selection bias in gene extraction on the basis of microarray gene-expression data”
Set up folds
Basically, the way to go is to wrap the entire feature selection and generalization error estimation process in a top-level loop of external cross validation. For 10-fold CV, we begin by defining which observations are in which folds.
nfold <- 10
nrows <- nrow(input)
folds <- rep(1:nfold, length.out = nrows)[sample(nrows)]
folds
#> [1] 5 6 3 8 1 6 9 6 6 5 4 3 6 3 4 2 1 7 2 10 6 3 5 1 6
#> [26] 10 9 10 10 1 8 7 10 9 7 1 7 6 4 4 8 10 6 3 7 9 10 3 1 5
#> [51] 9 4 3 10 10 8 4 3 1 9 6 6 3 8 2 5 5 7 5 9 7 7 8 9 2
#> [76] 8 4 1 1 10 2 9 6 9 7 6 3 4 10 5 1 2 6 9 6 10 1 7 1 5
#> [101] 9 9 4 8 1 2 9 2 5 4 4 3 8 8 5 4 4 1 2 2 7 2 6 8 4
#> [126] 7 2 3 8 1 6 5 3 10 8 4 10 9 2 8 10 1 10 9 7 2 1 3 2 3
#> [151] 9 1 8 9 2 1 6 7 5 4 7 2 7 6 8 3 2 5 10 2 5 4 8 7 7
#> [176] 3 2 5 1 9 5 10 9 4 8 8 3 5 7 3 3 4 5 8 2 5 4 6 6 10
#> [201] 7 7 10 3 4 8 5 1In R, many parallel functions like to operate on lists, so next we’ll reformat folds into a list, where each list element is a vector containing the test set indices for that fold.
folds <- split(seq_along(folds), folds)
folds
#> $`1`
#> [1] 5 17 24 30 36 49 59 78 79 91 97 99 105 118 130 142 147 152 156
#> [20] 179 208
#>
#> $`2`
#> [1] 16 19 65 75 81 92 106 108 119 120 122 127 139 146 149 155 162 167 170
#> [20] 177 195
#>
#> $`3`
#> [1] 3 12 14 22 44 48 53 58 63 87 112 128 133 148 150 166 176 187 190
#> [20] 191 204
#>
#> $`4`
#> [1] 11 15 39 40 52 57 77 88 103 110 111 116 117 125 136 160 172 184 192
#> [20] 197 205
#>
#> $`5`
#> [1] 1 10 23 50 66 67 69 90 100 109 115 132 159 168 171 178 181 188 193
#> [20] 196 207
#>
#> $`6`
#> [1] 2 6 8 9 13 21 25 38 43 61 62 83 86 93 95 123 131 157 164
#> [20] 198 199
#>
#> $`7`
#> [1] 18 32 35 37 45 68 71 72 85 98 121 126 145 158 161 163 174 175 189
#> [20] 201 202
#>
#> $`8`
#> [1] 4 31 41 56 64 73 76 104 113 114 124 129 135 140 153 165 173 185 186
#> [20] 194 206
#>
#> $`9`
#> [1] 7 27 34 46 51 60 70 74 82 84 94 101 102 107 138 144 151 154 180
#> [20] 183
#>
#> $`10`
#> [1] 20 26 28 29 33 42 47 54 55 80 89 96 134 137 141 143 169 182 200
#> [20] 203Perform feature ranking on all training sets
Using lapply, or one of its generic parallel cousins (ex: sge.parLapply from the Rsge package), we can now perform the feature ranking for all 10 training sets.
results <- lapply(folds, svmRFE.wrap, input, k = length(folds), halve.above = 100)
length(results)
#> [1] 10
head(results)
#> $`1`
#> $`1`$feature.ids
#> [1] 337 201 59 492 503 1 128 175 173 273 304 286 33 45 446 460 402 60
#> [19] 147 497 504 359 177 68 303 77 518 453 257 418 516 248 368 498 262 20
#> [37] 409 41 400 372 144 269 383 362 105 517 345 85 468 415 103 512 255 491
#> [55] 376 434 214 388 195 389 408 486 521 392 131 459 36 540 186 126 89 412
#> [73] 385 47 542 61 399 187 397 319 505 124 289 407 309 236 282 511 120 171
#> [91] 502 313 284 27 5 73 219 91 52 84 245 536 463 435 95 395 110 203
#> [109] 539 50 451 129 21 423 113 51 355 17 482 335 373 9 22 380 109 390
#> [127] 104 367 324 441 465 64 256 321 310 298 290 487 526 218 538 108 416 49
#> [145] 414 295 537 172 15 160 83 433 381 111 311 180 473 315 483 464 196 417
#> [163] 58 90 200 527 485 63 327 101 283 405 222 452 191 384 232 190 43 371
#> [181] 420 481 343 365 406 166 217 476 263 354 125 92 242 281 364 450 479 308
#> [199] 462 57 334 339 130 396 16 132 312 291 253 535 370 440 152 29 100 155
#> [217] 411 146 314 349 238 8 522 198 508 107 520 221 211 143 489 136 268 533
#> [235] 161 382 261 292 404 532 97 496 249 325 466 133 37 472 427 475 353 361
#> [253] 193 506 178 2 260 544 461 543 436 93 494 437 534 297 293 116 80 357
#> [271] 86 270 210 34 70 65 223 271 378 74 118 474 530 356 106 529 425 252
#> [289] 10 285 72 46 447 422 169 280 488 495 305 391 330 209 88 123 332 541
#> [307] 274 26 401 300 183 117 40 112 188 470 430 31 151 197 56 168 142 338
#> [325] 287 212 265 510 277 394 331 307 98 163 328 42 350 445 288 62 369 99
#> [343] 12 7 454 363 239 227 149 30 140 115 162 233 366 231 342 360 182 206
#> [361] 438 266 170 53 153 165 135 75 351 228 329 299 316 326 500 323 215 322
#> [379] 156 226 469 514 499 35 276 379 439 348 254 79 341 66 150 344 174 259
#> [397] 32 480 148 225 202 431 301 54 55 134 19 243 306 347 403 237 234 127
#> [415] 455 192 94 158 121 240 375 114 296 410 44 235 513 69 244 320 216 507
#> [433] 48 484 184 477 141 194 428 456 515 278 137 204 23 119 241 398 154 251
#> [451] 159 387 457 413 102 87 449 176 185 467 374 531 24 442 25 246 250 519
#> [469] 336 13 358 81 122 179 229 317 340 3 82 71 18 167 501 207 258 424
#> [487] 275 11 443 164 352 38 444 523 96 448 264 524 458 39 208 189 224 67
#> [505] 199 478 157 220 318 6 386 279 230 333 346 471 139 294 205 302 426 377
#> [523] 28 545 14 181 4 76 138 528 525 78 421 213 145 546 432 419 509 247
#> [541] 493 267 429 490 272 393
#>
#> $`1`$train.data.ids
#> [1] "1000804" "1023964" "1057962" "1099481" "1187766" "1208795" "1283494"
#> [8] "1320247" "1359325" "1435954" "1471736" "1497055" "1511464" "1517240"
#> [15] "1567356" "1737393" "1740607" "1780174" "1854959" "1875084" "1884448"
#> [22] "1934623" "1992284" "1995121" "2030383" "2054438" "2136051" "2230510"
#> [29] "2260910" "2306976" "2497695" "2682736" "2730704" "2735617" "2741068"
#> [36] "2773205" "2821683" "2854839" "2907383" "2950672" "2983819" "2991307"
#> [43] "2996531" "3163200" "3174224" "3235580" "3243657" "3349205" "3349423"
#> [50] "3433846" "3441455" "3457975" "3542588" "3601861" "3619797" "3650634"
#> [57] "3653737" "3679455" "3845761" "3999344" "4060823" "4079254" "4084645"
#> [64] "4095229" "4116166" "4154672" "4164316" "4187857" "4562206" "4827048"
#> [71] "6206397" "6568351" "8009688" "8415034" "8692452" "8697774" "8834383"
#> [78] "9326955" "9578663" "9750701" "9907452" "10004" "10016" "10009"
#> [85] "10010" "10012" "10020" "10022" "10023" "10028" "10030"
#> [92] "10038" "10031" "10032" "10035" "10037" "10039" "10042"
#> [99] "10044" "10050" "10051" "10052" "10053" "10056" "10058"
#> [106] "10059" "10054" "10048" "10060" "10047" "10062" "10064"
#> [113] "10065" "10066" "10068" "10119" "10109" "10110" "10111"
#> [120] "10112" "10107" "10019" "10077" "10078" "10079" "10080"
#> [127] "10014" "10089" "10090" "10091" "10045" "10093" "10094"
#> [134] "10095" "10097" "10098" "10099" "10101" "10102" "10108"
#> [141] "10002" "10011" "10113" "10114" "10115" "10006" "10105"
#> [148] "10024" "10106" "10116" "10117" "10118" "10120" "10026"
#> [155] "10121" "10122" "10123" "10082" "10074" "10076" "10103"
#> [162] "10081" "10083" "10084" "10085" "10036" "10086" "10027"
#> [169] "10087" "10025" "10029" "10017" "10049" "10070" "10071"
#> [176] "10033" "10072" "10073" "10104" "10088" "10040" "10124"
#> [183] "10125" "10007" "10126" "10127" "10128"
#>
#> $`1`$test.data.ids
#> [1] "1127915" "1700637" "1918630" "2107638" "2570769" "3011311" "3518345"
#> [8] "5164727" "5971050" "10001" "10018" "10021" "10034" "10057"
#> [15] "10069" "10008" "10092" "10096" "10100" "10075" "10129"
#>
#>
#> $`2`
#> $`2`$feature.ids
#> [1] 380 173 33 262 187 459 304 492 218 31 68 1 541 416 409 126 313 92
#> [19] 248 266 337 503 177 133 72 256 175 95 255 546 365 214 217 476 391 468
#> [37] 488 388 236 219 186 502 460 435 415 512 73 345 107 89 282 59 540 149
#> [55] 305 227 108 212 144 402 466 487 383 43 21 418 362 525 491 411 450 268
#> [73] 370 311 443 407 160 319 496 124 392 340 17 521 61 234 85 527 461 361
#> [91] 303 35 120 129 423 284 516 27 412 191 453 354 356 79 389 301 265 36
#> [109] 30 201 39 131 50 367 320 330 479 481 471 182 252 308 498 286 446 421
#> [127] 490 243 127 287 140 244 542 229 359 196 544 141 66 16 394 422 384 202
#> [145] 397 163 403 458 22 441 385 200 449 152 327 172 143 349 112 52 472 49
#> [163] 332 369 497 80 538 179 455 400 197 45 208 188 401 91 176 505 529 259
#> [181] 433 47 71 364 316 430 533 273 518 183 233 298 128 434 537 257 524 375
#> [199] 368 60 464 390 274 239 522 130 166 51 317 148 105 94 357 18 171 57
#> [217] 275 469 534 297 499 431 161 413 440 414 240 213 194 465 442 331 193 532
#> [235] 508 405 86 195 125 336 67 117 103 277 270 261 432 198 494 104 41 526
#> [253] 486 26 323 228 232 539 427 473 519 48 62 116 292 90 54 504 264 211
#> [271] 395 425 156 444 306 520 509 203 84 65 64 38 5 290 543 467 230 216
#> [289] 238 420 258 263 324 322 168 307 485 478 447 134 463 454 136 312 111 382
#> [307] 283 246 250 34 207 205 184 199 451 121 56 269 482 260 506 378 452 281
#> [325] 23 381 253 19 457 204 100 376 226 343 245 289 6 377 511 96 10 58
#> [343] 386 501 399 192 169 113 150 271 209 417 231 225 335 355 321 445 315 448
#> [361] 123 53 437 404 185 78 350 28 3 7 339 88 495 165 438 147 101 295
#> [379] 325 237 360 206 408 294 249 326 474 118 299 371 99 309 83 462 366 145
#> [397] 329 302 342 341 374 285 69 135 98 109 224 419 74 63 291 180 15 139
#> [415] 110 531 8 146 174 189 106 40 151 348 480 154 470 372 396 220 158 14
#> [433] 483 536 406 247 328 132 410 379 93 426 162 293 159 318 424 37 363 20
#> [451] 42 300 334 278 142 515 507 82 530 157 97 170 55 535 314 288 190 223
#> [469] 221 2 279 242 373 12 393 436 222 9 77 500 11 119 241 210 267 87
#> [487] 114 164 155 215 387 167 489 333 475 428 70 181 344 528 272 296 13 251
#> [505] 76 338 46 235 44 32 122 178 429 137 477 138 456 254 439 4 276 351
#> [523] 347 29 24 346 352 353 280 484 153 81 517 358 310 75 514 510 545 398
#> [541] 115 102 513 25 493 523
#>
#> $`2`$train.data.ids
#> [1] "1000804" "1023964" "1057962" "1099481" "1127915" "1187766" "1208795"
#> [8] "1283494" "1320247" "1359325" "1435954" "1471736" "1497055" "1511464"
#> [15] "1517240" "1700637" "1737393" "1780174" "1854959" "1875084" "1884448"
#> [22] "1918630" "1934623" "1992284" "1995121" "2030383" "2054438" "2107638"
#> [29] "2136051" "2230510" "2260910" "2306976" "2497695" "2570769" "2682736"
#> [36] "2730704" "2735617" "2741068" "2773205" "2821683" "2854839" "2907383"
#> [43] "2950672" "2983819" "2991307" "2996531" "3011311" "3163200" "3174224"
#> [50] "3235580" "3243657" "3349205" "3349423" "3433846" "3441455" "3457975"
#> [57] "3518345" "3542588" "3601861" "3619797" "3650634" "3653737" "3845761"
#> [64] "3999344" "4060823" "4079254" "4084645" "4095229" "4116166" "4154672"
#> [71] "4164316" "4562206" "4827048" "5164727" "5971050" "6206397" "8009688"
#> [78] "8415034" "8692452" "8697774" "8834383" "9326955" "9578663" "9750701"
#> [85] "9907452" "10001" "10016" "10009" "10010" "10012" "10018"
#> [92] "10020" "10021" "10022" "10023" "10028" "10030" "10038"
#> [99] "10034" "10032" "10037" "10039" "10042" "10044" "10050"
#> [106] "10051" "10052" "10053" "10056" "10057" "10054" "10060"
#> [113] "10047" "10062" "10064" "10066" "10068" "10069" "10119"
#> [120] "10109" "10110" "10111" "10112" "10107" "10019" "10077"
#> [127] "10079" "10080" "10008" "10014" "10089" "10090" "10092"
#> [134] "10045" "10094" "10095" "10096" "10097" "10098" "10100"
#> [141] "10101" "10102" "10108" "10002" "10011" "10114" "10115"
#> [148] "10006" "10105" "10106" "10116" "10118" "10120" "10026"
#> [155] "10121" "10122" "10123" "10074" "10075" "10076" "10103"
#> [162] "10081" "10083" "10084" "10085" "10036" "10086" "10027"
#> [169] "10087" "10025" "10029" "10017" "10049" "10070" "10033"
#> [176] "10072" "10073" "10104" "10088" "10040" "10124" "10125"
#> [183] "10007" "10126" "10127" "10128" "10129"
#>
#> $`2`$test.data.ids
#> [1] "1567356" "1740607" "3679455" "4187857" "6568351" "10004" "10031"
#> [8] "10035" "10058" "10059" "10048" "10065" "10078" "10091"
#> [15] "10093" "10099" "10113" "10024" "10117" "10082" "10071"
#>
#>
#> $`3`
#> $`3`$feature.ids
#> [1] 337 201 1 36 518 173 262 62 90 187 340 175 128 129 203 256 68 172
#> [19] 391 217 219 113 92 147 313 107 460 362 255 468 479 466 441 497 383 263
#> [37] 144 365 453 95 408 409 332 301 191 181 432 491 421 268 504 122 60 512
#> [55] 345 481 540 269 314 527 22 244 415 492 376 200 459 440 399 392 120 186
#> [73] 418 45 319 388 41 27 65 357 446 478 252 405 470 498 117 265 94 26
#> [91] 544 532 412 486 33 359 397 350 248 422 542 371 503 246 276 49 464 318
#> [109] 85 402 153 416 521 281 99 227 133 43 482 169 473 303 282 180 72 434
#> [127] 59 451 61 513 230 496 218 355 431 511 378 12 66 420 293 103 253 130
#> [145] 160 395 21 450 136 374 396 516 356 100 284 505 411 208 407 222 385 50
#> [163] 216 266 349 234 382 389 273 37 528 140 179 108 274 233 86 35 321 406
#> [181] 286 533 192 297 423 236 520 425 126 283 16 251 177 449 73 306 384 381
#> [199] 159 232 472 183 195 348 502 112 361 47 463 419 149 125 546 295 367 353
#> [217] 158 213 243 91 176 325 427 15 40 461 475 84 10 57 509 487 435 400
#> [235] 442 338 51 124 67 257 188 538 430 525 329 202 210 360 438 312 64 522
#> [253] 245 310 46 448 78 401 379 83 476 161 123 336 483 316 524 322 5 197
#> [271] 334 155 198 424 287 539 196 54 141 52 537 89 275 82 292 485 205 3
#> [289] 19 278 471 167 199 209 444 114 211 207 364 190 343 237 231 433 39 331
#> [307] 121 366 403 18 280 291 20 8 465 369 17 523 58 304 393 543 285 105
#> [325] 238 212 214 294 484 97 194 333 429 32 488 307 2 98 390 42 118 150
#> [343] 154 320 469 111 193 24 455 308 462 104 347 55 375 258 157 309 101 182
#> [361] 536 277 510 452 354 146 501 109 9 53 131 206 189 166 88 69 134 259
#> [379] 215 74 75 489 457 506 151 339 260 261 127 417 515 110 426 529 351 341
#> [397] 29 352 443 414 404 6 377 323 170 132 494 116 63 507 71 330 242 477
#> [415] 413 264 508 96 168 305 317 31 467 526 541 335 119 447 38 249 184 28
#> [433] 342 535 514 531 79 386 517 81 137 174 445 250 185 224 519 439 380 145
#> [451] 410 225 80 296 372 229 272 226 178 315 13 239 143 270 70 370 235 493
#> [469] 490 48 34 76 87 204 456 4 221 288 165 290 115 289 327 163 228 299
#> [487] 387 436 241 44 267 368 102 326 30 474 23 344 138 254 302 545 77 152
#> [505] 56 428 156 500 164 328 25 271 142 300 14 311 398 139 437 247 240 495
#> [523] 7 394 346 298 93 363 220 454 162 279 106 148 373 358 223 11 324 480
#> [541] 499 458 530 135 171 534
#>
#> $`3`$train.data.ids
#> [1] "1000804" "1023964" "1099481" "1127915" "1187766" "1208795" "1283494"
#> [8] "1320247" "1359325" "1435954" "1497055" "1517240" "1567356" "1700637"
#> [15] "1737393" "1740607" "1780174" "1854959" "1884448" "1918630" "1934623"
#> [22] "1992284" "1995121" "2030383" "2054438" "2107638" "2136051" "2230510"
#> [29] "2260910" "2306976" "2497695" "2570769" "2682736" "2730704" "2735617"
#> [36] "2741068" "2773205" "2821683" "2854839" "2950672" "2983819" "2991307"
#> [43] "3011311" "3163200" "3174224" "3235580" "3349205" "3349423" "3433846"
#> [50] "3441455" "3518345" "3542588" "3601861" "3619797" "3653737" "3679455"
#> [57] "3845761" "3999344" "4060823" "4079254" "4084645" "4095229" "4116166"
#> [64] "4154672" "4164316" "4187857" "4562206" "4827048" "5164727" "5971050"
#> [71] "6206397" "6568351" "8009688" "8415034" "8692452" "8697774" "8834383"
#> [78] "9578663" "9750701" "9907452" "10001" "10004" "10016" "10009"
#> [85] "10010" "10012" "10018" "10020" "10021" "10022" "10023"
#> [92] "10028" "10030" "10038" "10034" "10031" "10032" "10035"
#> [99] "10037" "10039" "10042" "10050" "10051" "10052" "10053"
#> [106] "10056" "10057" "10058" "10059" "10054" "10048" "10060"
#> [113] "10047" "10062" "10064" "10065" "10068" "10069" "10119"
#> [120] "10109" "10111" "10112" "10107" "10019" "10077" "10078"
#> [127] "10079" "10080" "10008" "10014" "10089" "10090" "10091"
#> [134] "10092" "10093" "10095" "10096" "10097" "10098" "10099"
#> [141] "10100" "10101" "10102" "10108" "10002" "10011" "10113"
#> [148] "10114" "10115" "10006" "10024" "10106" "10116" "10117"
#> [155] "10118" "10120" "10026" "10121" "10122" "10082" "10074"
#> [162] "10075" "10076" "10103" "10081" "10083" "10084" "10085"
#> [169] "10036" "10027" "10087" "10017" "10049" "10070" "10071"
#> [176] "10033" "10072" "10073" "10104" "10088" "10040" "10124"
#> [183] "10125" "10126" "10127" "10128" "10129"
#>
#> $`3`$test.data.ids
#> [1] "1057962" "1471736" "1511464" "1875084" "2907383" "2996531" "3243657"
#> [8] "3457975" "3650634" "9326955" "10044" "10066" "10110" "10045"
#> [15] "10094" "10105" "10123" "10086" "10025" "10029" "10007"
#>
#>
#> $`4`
#> $`4`$feature.ids
#> [1] 262 397 33 319 337 173 382 108 90 128 511 130 85 203 136 133 184 383
#> [19] 283 186 512 522 89 479 463 140 58 460 485 411 331 308 218 172 339 219
#> [37] 266 126 368 504 362 105 236 498 255 363 45 207 92 415 66 435 281 304
#> [55] 390 402 180 65 103 360 109 68 422 263 395 428 349 354 468 117 303 284
#> [73] 27 212 41 492 542 497 22 473 269 144 477 259 502 452 95 418 412 370
#> [91] 229 268 187 532 391 265 396 388 174 200 505 405 392 481 113 453 385 176
#> [109] 525 356 274 47 400 491 486 59 437 150 208 253 240 409 201 295 32 194
#> [127] 72 62 305 205 459 177 376 164 399 503 352 403 101 124 282 475 521 367
#> [145] 163 244 257 17 464 149 508 381 100 446 313 162 476 67 34 416 125 28
#> [163] 373 114 1 273 537 344 57 267 60 158 49 77 544 120 355 147 198 87
#> [181] 527 110 196 351 232 407 287 474 35 369 191 40 175 361 36 359 340 297
#> [199] 71 434 286 472 251 107 332 483 441 153 292 94 2 499 197 448 3 8
#> [217] 51 524 104 256 488 432 494 518 378 470 301 450 365 129 86 43 46 298
#> [235] 245 171 21 465 461 447 183 496 289 223 350 9 278 425 193 546 258 195
#> [253] 44 357 293 478 155 540 123 42 520 315 336 327 404 167 83 48 55 462
#> [271] 26 96 442 134 264 211 316 440 353 419 270 189 509 311 54 406 76 216
#> [289] 156 222 141 127 261 489 429 414 466 154 330 170 325 515 545 271 506 445
#> [307] 541 384 148 529 514 487 536 220 214 221 210 217 533 469 79 169 321 131
#> [325] 424 166 151 386 18 366 227 342 234 455 454 444 516 118 237 343 246 16
#> [343] 401 467 543 314 307 277 188 457 160 364 249 209 235 387 329 238 374 393
#> [361] 280 433 398 410 202 111 309 490 230 142 112 52 190 276 146 73 84 24
#> [379] 317 242 31 310 15 335 239 93 115 348 137 318 204 260 371 159 300 165
#> [397] 91 493 389 334 25 417 226 526 517 39 157 241 5 182 458 106 78 495
#> [415] 228 7 275 534 338 528 4 224 38 243 539 456 420 426 372 145 63 152
#> [433] 530 484 225 192 531 14 199 328 178 252 501 380 322 449 61 375 138 97
#> [451] 482 439 296 70 347 30 408 358 19 294 231 50 288 82 500 248 320 69
#> [469] 102 507 13 430 538 306 64 436 513 161 254 98 451 135 119 122 80 438
#> [487] 431 37 75 413 523 326 143 213 168 341 345 139 279 185 233 181 535 179
#> [505] 121 81 74 302 12 56 285 132 88 53 116 312 323 290 272 377 421 206
#> [523] 6 29 480 394 250 471 215 20 23 324 10 346 11 379 519 247 299 291
#> [541] 333 99 427 443 510 423
#>
#> $`4`$train.data.ids
#> [1] "1000804" "1023964" "1057962" "1099481" "1127915" "1187766" "1208795"
#> [8] "1283494" "1320247" "1359325" "1471736" "1497055" "1511464" "1567356"
#> [15] "1700637" "1737393" "1740607" "1780174" "1854959" "1875084" "1884448"
#> [22] "1918630" "1934623" "1992284" "1995121" "2030383" "2054438" "2107638"
#> [29] "2136051" "2230510" "2260910" "2306976" "2497695" "2570769" "2682736"
#> [36] "2730704" "2773205" "2821683" "2854839" "2907383" "2950672" "2983819"
#> [43] "2991307" "2996531" "3011311" "3163200" "3174224" "3243657" "3349205"
#> [50] "3349423" "3433846" "3457975" "3518345" "3542588" "3601861" "3619797"
#> [57] "3650634" "3653737" "3679455" "3845761" "3999344" "4060823" "4079254"
#> [64] "4084645" "4095229" "4116166" "4154672" "4164316" "4187857" "4562206"
#> [71] "5164727" "5971050" "6206397" "6568351" "8009688" "8415034" "8692452"
#> [78] "8697774" "8834383" "9326955" "9750701" "9907452" "10001" "10004"
#> [85] "10016" "10009" "10010" "10012" "10018" "10020" "10021"
#> [92] "10022" "10023" "10028" "10038" "10034" "10031" "10032"
#> [99] "10035" "10037" "10044" "10050" "10051" "10052" "10057"
#> [106] "10058" "10059" "10054" "10048" "10060" "10047" "10064"
#> [113] "10065" "10066" "10068" "10069" "10119" "10109" "10110"
#> [120] "10111" "10112" "10019" "10077" "10078" "10079" "10080"
#> [127] "10008" "10014" "10089" "10090" "10091" "10092" "10045"
#> [134] "10093" "10094" "10095" "10096" "10097" "10098" "10099"
#> [141] "10100" "10101" "10102" "10108" "10011" "10113" "10114"
#> [148] "10115" "10006" "10105" "10024" "10106" "10116" "10117"
#> [155] "10118" "10026" "10121" "10122" "10123" "10082" "10074"
#> [162] "10075" "10076" "10103" "10081" "10083" "10085" "10036"
#> [169] "10086" "10027" "10087" "10025" "10029" "10049" "10070"
#> [176] "10071" "10033" "10073" "10104" "10088" "10040" "10124"
#> [183] "10125" "10007" "10127" "10128" "10129"
#>
#> $`4`$test.data.ids
#> [1] "1435954" "1517240" "2735617" "2741068" "3235580" "3441455" "4827048"
#> [8] "9578663" "10030" "10039" "10042" "10053" "10056" "10062"
#> [15] "10107" "10002" "10120" "10084" "10017" "10072" "10126"
#>
#>
#> $`5`
#> $`5`$feature.ids
#> [1] 173 337 304 262 402 544 175 1 59 63 418 94 129 205 108 502 512 504
#> [19] 35 503 128 177 335 46 412 492 345 287 327 181 527 409 505 542 460 319
#> [37] 140 169 391 450 468 282 395 73 43 388 405 359 68 465 497 479 100 362
#> [55] 191 364 354 321 453 368 49 508 266 66 217 61 360 434 422 473 200 212
#> [73] 95 520 291 491 105 303 172 532 244 109 355 168 47 414 144 313 298 452
#> [91] 27 45 219 378 537 389 70 501 201 448 119 111 256 187 206 147 466 459
#> [109] 361 521 343 392 41 26 415 379 308 440 149 464 207 411 74 127 310 518
#> [127] 180 186 136 397 446 123 463 198 107 451 131 485 114 257 55 232 407 106
#> [145] 163 146 195 478 227 325 231 383 381 264 408 545 390 356 179 259 50 410
#> [163] 33 103 522 311 400 118 89 369 416 332 255 539 60 120 423 403 437 324
#> [181] 192 384 199 349 183 396 78 292 546 274 336 220 376 498 36 523 506 441
#> [199] 30 44 253 252 525 524 263 510 40 270 71 154 288 435 281 13 90 218
#> [217] 461 29 353 417 385 329 101 449 124 83 514 444 318 138 184 267 331 301
#> [235] 320 286 476 32 277 197 543 22 162 57 242 80 64 21 469 526 365 275
#> [253] 110 171 511 261 52 424 159 196 346 406 233 457 386 228 538 97 152 370
#> [271] 529 443 494 425 285 509 91 221 135 419 295 305 367 99 248 439 279 350
#> [289] 6 160 394 438 348 82 69 122 316 189 182 75 273 3 203 528 276 126
#> [307] 234 401 380 399 420 284 481 513 315 475 229 299 216 170 112 404 246 429
#> [325] 358 507 382 145 540 333 306 293 516 247 236 535 474 98 18 208 372 9
#> [343] 330 338 48 211 351 300 312 178 536 137 240 151 241 5 366 230 499 445
#> [361] 117 515 375 188 398 209 25 283 302 77 79 125 202 51 134 260 428 7
#> [379] 150 161 2 14 96 489 85 113 442 20 225 190 65 222 237 226 250 54
#> [397] 426 534 16 317 4 530 344 224 104 339 363 92 323 194 377 352 347 533
#> [415] 238 322 116 155 484 166 167 371 56 373 37 185 271 436 342 387 132 156
#> [433] 53 8 431 393 483 28 72 143 23 251 519 204 289 130 500 235 12 487
#> [451] 265 84 15 413 472 296 427 193 374 76 268 541 309 328 158 269 62 38
#> [469] 517 86 477 447 490 24 462 17 139 121 334 433 272 93 280 245 88 133
#> [487] 239 157 42 214 531 307 314 34 87 432 174 341 141 480 102 148 249 493
#> [505] 254 81 326 294 31 176 210 467 297 456 458 495 488 482 486 455 153 258
#> [523] 340 471 454 278 421 11 165 290 39 470 357 496 223 215 10 213 115 164
#> [541] 67 58 430 19 142 243
#>
#> $`5`$train.data.ids
#> [1] "1023964" "1057962" "1099481" "1127915" "1187766" "1208795" "1283494"
#> [8] "1320247" "1435954" "1471736" "1497055" "1511464" "1517240" "1567356"
#> [15] "1700637" "1737393" "1740607" "1780174" "1854959" "1875084" "1918630"
#> [22] "1934623" "1992284" "1995121" "2030383" "2054438" "2107638" "2136051"
#> [29] "2230510" "2260910" "2306976" "2497695" "2570769" "2682736" "2730704"
#> [36] "2735617" "2741068" "2773205" "2821683" "2854839" "2907383" "2950672"
#> [43] "2983819" "2991307" "2996531" "3011311" "3174224" "3235580" "3243657"
#> [50] "3349205" "3349423" "3433846" "3441455" "3457975" "3518345" "3542588"
#> [57] "3601861" "3619797" "3650634" "3653737" "3679455" "4060823" "4084645"
#> [64] "4095229" "4116166" "4154672" "4164316" "4187857" "4562206" "4827048"
#> [71] "5164727" "5971050" "6206397" "6568351" "8009688" "8415034" "8692452"
#> [78] "8697774" "8834383" "9326955" "9578663" "9750701" "10001" "10004"
#> [85] "10016" "10009" "10010" "10012" "10018" "10020" "10021"
#> [92] "10023" "10028" "10030" "10038" "10034" "10031" "10032"
#> [99] "10035" "10039" "10042" "10044" "10050" "10051" "10053"
#> [106] "10056" "10057" "10058" "10059" "10054" "10048" "10060"
#> [113] "10047" "10062" "10064" "10065" "10066" "10068" "10069"
#> [120] "10119" "10110" "10111" "10112" "10107" "10019" "10077"
#> [127] "10078" "10079" "10080" "10008" "10014" "10089" "10090"
#> [134] "10091" "10092" "10045" "10093" "10094" "10095" "10096"
#> [141] "10097" "10098" "10099" "10100" "10101" "10102" "10002"
#> [148] "10011" "10113" "10114" "10115" "10006" "10105" "10024"
#> [155] "10116" "10117" "10120" "10026" "10121" "10122" "10123"
#> [162] "10082" "10075" "10076" "10081" "10083" "10084" "10085"
#> [169] "10036" "10086" "10087" "10025" "10029" "10017" "10070"
#> [176] "10071" "10072" "10073" "10104" "10088" "10040" "10124"
#> [183] "10125" "10007" "10126" "10127" "10129"
#>
#> $`5`$test.data.ids
#> [1] "1000804" "1359325" "1884448" "3163200" "3845761" "3999344" "4079254"
#> [8] "9907452" "10022" "10037" "10052" "10109" "10108" "10106"
#> [15] "10118" "10074" "10103" "10027" "10049" "10033" "10128"
#>
#>
#> $`6`
#> $`6`$feature.ids
#> [1] 262 337 173 304 33 130 255 521 308 41 22 286 175 157 120 95 365 140
#> [19] 8 319 43 187 218 479 383 1 79 487 243 497 542 228 259 38 352 169
#> [37] 395 434 77 21 265 183 502 466 105 19 504 185 388 524 405 411 59 31
#> [55] 62 16 392 171 144 357 345 73 397 52 313 409 520 498 468 402 396 491
#> [73] 186 460 422 453 544 511 536 391 385 273 27 89 85 172 113 436 440 68
#> [91] 129 532 441 384 446 486 45 342 403 127 505 314 128 473 107 293 518 149
#> [109] 478 227 188 519 459 452 181 256 415 219 496 375 546 203 195 418 253 508
#> [127] 214 201 216 198 199 281 370 354 355 86 378 36 492 261 91 245 356 217
#> [145] 509 117 249 103 420 537 83 112 465 194 231 360 488 271 513 104 47 361
#> [163] 512 463 133 349 442 389 12 213 124 516 343 143 257 278 266 341 449 425
#> [181] 230 285 426 503 450 432 90 335 232 49 34 506 274 527 398 190 39 329
#> [199] 139 412 110 282 367 53 381 364 60 63 407 244 207 481 131 270 435 239
#> [217] 305 353 427 212 191 65 464 303 525 366 141 406 69 289 454 401 347 279
#> [235] 386 202 176 288 145 177 235 495 526 17 309 5 371 135 263 161 538 246
#> [253] 500 334 445 423 295 84 283 108 205 267 179 543 416 61 330 200 539 475
#> [271] 275 534 344 25 501 390 121 456 2 322 136 528 87 67 72 469 101 380
#> [289] 193 269 535 209 368 480 237 419 56 376 116 210 32 291 15 10 522 310
#> [307] 74 44 50 93 9 350 197 206 196 154 290 147 238 132 248 280 221 444
#> [325] 184 76 251 46 467 387 264 215 80 111 240 180 321 404 160 530 11 115
#> [343] 40 94 58 55 541 301 150 408 429 424 170 348 159 92 483 82 312 54
#> [361] 134 99 451 358 81 146 29 316 447 363 472 51 226 306 461 88 443 458
#> [379] 64 223 299 470 336 437 277 125 260 302 455 448 57 254 225 297 158 373
#> [397] 431 340 323 531 109 151 30 417 477 324 482 163 333 97 433 14 123 414
#> [415] 48 529 174 18 327 26 377 211 476 372 540 102 192 494 272 153 252 126
#> [433] 328 317 276 78 346 167 507 413 66 242 318 287 42 156 490 462 138 70
#> [451] 428 400 122 165 307 35 258 332 485 100 374 182 489 474 189 421 7 284
#> [469] 331 471 118 114 320 362 294 457 166 24 292 152 514 300 164 296 545 119
#> [487] 298 222 325 484 499 37 142 155 379 359 178 523 162 3 106 71 399 234
#> [505] 339 393 351 6 439 515 250 315 229 98 247 236 533 233 204 394 224 168
#> [523] 369 311 20 137 208 241 23 382 510 220 4 75 493 28 326 438 410 268
#> [541] 517 338 430 148 96 13
#>
#> $`6`$train.data.ids
#> [1] "1000804" "1057962" "1099481" "1127915" "1208795" "1359325" "1435954"
#> [8] "1471736" "1511464" "1517240" "1567356" "1700637" "1737393" "1740607"
#> [15] "1780174" "1875084" "1884448" "1918630" "1992284" "1995121" "2030383"
#> [22] "2054438" "2107638" "2136051" "2230510" "2260910" "2306976" "2497695"
#> [29] "2570769" "2682736" "2735617" "2741068" "2773205" "2821683" "2907383"
#> [36] "2950672" "2983819" "2991307" "2996531" "3011311" "3163200" "3174224"
#> [43] "3235580" "3243657" "3349205" "3349423" "3433846" "3441455" "3457975"
#> [50] "3518345" "3542588" "3650634" "3653737" "3679455" "3845761" "3999344"
#> [57] "4060823" "4079254" "4084645" "4095229" "4116166" "4154672" "4164316"
#> [64] "4187857" "4562206" "4827048" "5164727" "5971050" "6206397" "6568351"
#> [71] "8009688" "8692452" "8697774" "9326955" "9578663" "9750701" "9907452"
#> [78] "10001" "10004" "10009" "10012" "10018" "10020" "10021"
#> [85] "10022" "10023" "10028" "10030" "10038" "10034" "10031"
#> [92] "10032" "10035" "10037" "10039" "10042" "10044" "10050"
#> [99] "10051" "10052" "10053" "10056" "10057" "10058" "10059"
#> [106] "10054" "10048" "10047" "10062" "10064" "10065" "10066"
#> [113] "10068" "10069" "10109" "10110" "10111" "10112" "10107"
#> [120] "10019" "10077" "10078" "10079" "10080" "10008" "10014"
#> [127] "10089" "10090" "10091" "10092" "10045" "10093" "10094"
#> [134] "10095" "10096" "10097" "10098" "10099" "10100" "10102"
#> [141] "10108" "10002" "10011" "10113" "10114" "10006" "10105"
#> [148] "10024" "10106" "10116" "10117" "10118" "10120" "10026"
#> [155] "10121" "10122" "10123" "10082" "10074" "10075" "10076"
#> [162] "10103" "10081" "10083" "10084" "10085" "10036" "10086"
#> [169] "10027" "10087" "10025" "10029" "10017" "10049" "10070"
#> [176] "10071" "10033" "10072" "10088" "10040" "10124" "10125"
#> [183] "10007" "10126" "10127" "10128" "10129"
#>
#> $`6`$test.data.ids
#> [1] "1023964" "1187766" "1283494" "1320247" "1497055" "1854959" "1934623"
#> [8] "2730704" "2854839" "3601861" "3619797" "8415034" "8834383" "10016"
#> [15] "10010" "10060" "10119" "10101" "10115" "10073" "10104"Each list element in results contains the feature rankings for that fold (feature.ids), as well as the training set row names used to obtain them (train.data.ids). The remaining test set row names are included as well (test.data.ids).
Obtain top features across all folds
If we were going to apply these findings to a final test set somewhere, we would still want the best features across all of this training data.
top.features <- WriteFeatures(results, input, save=FALSE)
plot(top.features$AvgRank)
Ordered by average rank across the 10 folds (AvgRank, lower numbers are better), this gives us a list of the feature names (FeatureName, i.e. the corresponding column name from input), as well as the feature indices (FeatureID, i.e. the corresponding column index from input minus 1).
Estimate generalization error using a varying number of top features
Now that we have a ranking of features for each of the 10 training sets, the final step is to estimate the generalization error we can expect if we were to train a final classifier on these features and apply it to a new test set. Here, a radial basis function kernel SVM is tuned on each training set independently. This consists of doing internal 10-fold CV error estimation at each combination of SVM hyperparameters (Cost and Gamma) using grid search. The optimal parameters are then used to train the SVM on the entire training set. Finally, generalization error is determined by predicting the corresponding test set. This is done for each fold in the external 10-fold CV, and all 10 of these generalization error estimates are averaged to give more stability. This process is repeated while varying the number of top features that are used as input, and there will typically be a “sweet spot” where there are not too many nor too few features. Outlined, this process looks like:
external 10x CV
Rank features with mSVM-RFE
for(nfeat=1 to 500ish)
Grid search over SVM parameters
10x CV
Train SVM
Obtain generalization error estimate
Average generalization error estimate across multiple folds
Choose parameters with best average performance
Train SVM on full training set
Obtain generalization error estimate on corresponding external CV test set
Average generalization errors across multiple folds
Choose the optimum number of featuresTo implement it over the top 5 features, we do:
featsweep <- lapply(1:5, FeatSweep.wrap, results, input)
featsweep
#> [[1]]
#> [[1]]$svm.list
#> [[1]]$svm.list$`1`
#> gamma cost error dispersion
#> 1 0.03125 64 0.4761905 NA
#>
#> [[1]]$svm.list$`2`
#> gamma cost error dispersion
#> 1 0.0002441406 0.015625 0.6190476 NA
#>
#> [[1]]$svm.list$`3`
#> gamma cost error dispersion
#> 1 1 4 0.4761905 NA
#>
#> [[1]]$svm.list$`4`
#> gamma cost error dispersion
#> 1 1 1 0.3333333 NA
#>
#> [[1]]$svm.list$`5`
#> gamma cost error dispersion
#> 1 0.5 0.5 0.3809524 NA
#>
#> [[1]]$svm.list$`6`
#> gamma cost error dispersion
#> 1 0.001953125 64 0.5238095 NA
#>
#> [[1]]$svm.list$`7`
#> gamma cost error dispersion
#> 1 0.0078125 32 0.4285714 NA
#>
#> [[1]]$svm.list$`8`
#> gamma cost error dispersion
#> 1 0.25 0.125 0.4761905 NA
#>
#> [[1]]$svm.list$`9`
#> gamma cost error dispersion
#> 1 1 16 0.6 NA
#>
#> [[1]]$svm.list$`10`
#> gamma cost error dispersion
#> 1 0.5 0.5 0.45 NA
#>
#>
#> [[1]]$error
#> [1] 0.4764286
#>
#>
#> [[2]]
#> [[2]]$svm.list
#> [[2]]$svm.list$`1`
#> gamma cost error dispersion
#> 1 0.015625 64 0.2857143 NA
#>
#> [[2]]$svm.list$`2`
#> gamma cost error dispersion
#> 1 0.25 8 0.6190476 NA
#>
#> [[2]]$svm.list$`3`
#> gamma cost error dispersion
#> 1 0.015625 8 0.4285714 NA
#>
#> [[2]]$svm.list$`4`
#> gamma cost error dispersion
#> 1 0.5 32 0.3333333 NA
#>
#> [[2]]$svm.list$`5`
#> gamma cost error dispersion
#> 1 0.03125 16 0.3809524 NA
#>
#> [[2]]$svm.list$`6`
#> gamma cost error dispersion
#> 1 0.0625 1 0.4761905 NA
#>
#> [[2]]$svm.list$`7`
#> gamma cost error dispersion
#> 1 0.25 32 0.3809524 NA
#>
#> [[2]]$svm.list$`8`
#> gamma cost error dispersion
#> 1 0.25 1 0.4285714 NA
#>
#> [[2]]$svm.list$`9`
#> gamma cost error dispersion
#> 1 1 32 0.5 NA
#>
#> [[2]]$svm.list$`10`
#> gamma cost error dispersion
#> 1 0.0078125 16 0.45 NA
#>
#>
#> [[2]]$error
#> [1] 0.4283333
#>
#>
#> [[3]]
#> [[3]]$svm.list
#> [[3]]$svm.list$`1`
#> gamma cost error dispersion
#> 1 0.125 32 0.2857143 NA
#>
#> [[3]]$svm.list$`2`
#> gamma cost error dispersion
#> 1 0.0625 16 0.5238095 NA
#>
#> [[3]]$svm.list$`3`
#> gamma cost error dispersion
#> 1 0.25 0.25 0.3333333 NA
#>
#> [[3]]$svm.list$`4`
#> gamma cost error dispersion
#> 1 0.5 1 0.2857143 NA
#>
#> [[3]]$svm.list$`5`
#> gamma cost error dispersion
#> 1 0.0625 16 0.4761905 NA
#>
#> [[3]]$svm.list$`6`
#> gamma cost error dispersion
#> 1 0.015625 4 0.4285714 NA
#>
#> [[3]]$svm.list$`7`
#> gamma cost error dispersion
#> 1 0.25 16 0.4285714 NA
#>
#> [[3]]$svm.list$`8`
#> gamma cost error dispersion
#> 1 0.5 32 0.3809524 NA
#>
#> [[3]]$svm.list$`9`
#> gamma cost error dispersion
#> 1 0.0625 32 0.3 NA
#>
#> [[3]]$svm.list$`10`
#> gamma cost error dispersion
#> 1 0.25 16 0.5 NA
#>
#>
#> [[3]]$error
#> [1] 0.3942857
#>
#>
#> [[4]]
#> [[4]]$svm.list
#> [[4]]$svm.list$`1`
#> gamma cost error dispersion
#> 1 0.125 2 0.3809524 NA
#>
#> [[4]]$svm.list$`2`
#> gamma cost error dispersion
#> 1 0.125 32 0.4761905 NA
#>
#> [[4]]$svm.list$`3`
#> gamma cost error dispersion
#> 1 0.015625 64 0.4285714 NA
#>
#> [[4]]$svm.list$`4`
#> gamma cost error dispersion
#> 1 0.125 16 0.2857143 NA
#>
#> [[4]]$svm.list$`5`
#> gamma cost error dispersion
#> 1 0.03125 8 0.3333333 NA
#>
#> [[4]]$svm.list$`6`
#> gamma cost error dispersion
#> 1 0.0625 1 0.3809524 NA
#>
#> [[4]]$svm.list$`7`
#> gamma cost error dispersion
#> 1 0.03125 16 0.4285714 NA
#>
#> [[4]]$svm.list$`8`
#> gamma cost error dispersion
#> 1 0.125 8 0.3809524 NA
#>
#> [[4]]$svm.list$`9`
#> gamma cost error dispersion
#> 1 0.125 2 0.3 NA
#>
#> [[4]]$svm.list$`10`
#> gamma cost error dispersion
#> 1 0.125 32 0.4 NA
#>
#>
#> [[4]]$error
#> [1] 0.3795238
#>
#>
#> [[5]]
#> [[5]]$svm.list
#> [[5]]$svm.list$`1`
#> gamma cost error dispersion
#> 1 0.0625 16 0.2380952 NA
#>
#> [[5]]$svm.list$`2`
#> gamma cost error dispersion
#> 1 0.0078125 16 0.4285714 NA
#>
#> [[5]]$svm.list$`3`
#> gamma cost error dispersion
#> 1 0.0625 8 0.4761905 NA
#>
#> [[5]]$svm.list$`4`
#> gamma cost error dispersion
#> 1 0.03125 4 0.2380952 NA
#>
#> [[5]]$svm.list$`5`
#> gamma cost error dispersion
#> 1 0.0625 1 0.2857143 NA
#>
#> [[5]]$svm.list$`6`
#> gamma cost error dispersion
#> 1 0.25 0.5 0.4285714 NA
#>
#> [[5]]$svm.list$`7`
#> gamma cost error dispersion
#> 1 0.03125 1 0.3333333 NA
#>
#> [[5]]$svm.list$`8`
#> gamma cost error dispersion
#> 1 0.00390625 32 0.4285714 NA
#>
#> [[5]]$svm.list$`9`
#> gamma cost error dispersion
#> 1 0.0078125 64 0.35 NA
#>
#> [[5]]$svm.list$`10`
#> gamma cost error dispersion
#> 1 0.25 2 0.55 NA
#>
#>
#> [[5]]$error
#> [1] 0.3757143Each featsweep list element corresponds to using that many of the top features (i.e. featsweep[1] is using only the top feature, featsweep[2] is using the top 2 features, etc.). Within each, svm.list contains the generalization error estimates for each of the 10 folds in the external 10-fold CV. These accuracies are averaged as error.
Plot of generalization error vs. # of features
To show these results visually, we can plot the average generalization error vs. the number of top features used as input.
For reference, it is useful to show the chance error rate. Typically, this is equal to the “no information” rate we would get if we simply always picked the class label with the greater prevalence in the data set.
no.info <- min(prop.table(table(input[,1])))
errors <- sapply(featsweep, function(x) ifelse(is.null(x), NA, x$error))
PlotErrors(errors, no.info=no.info)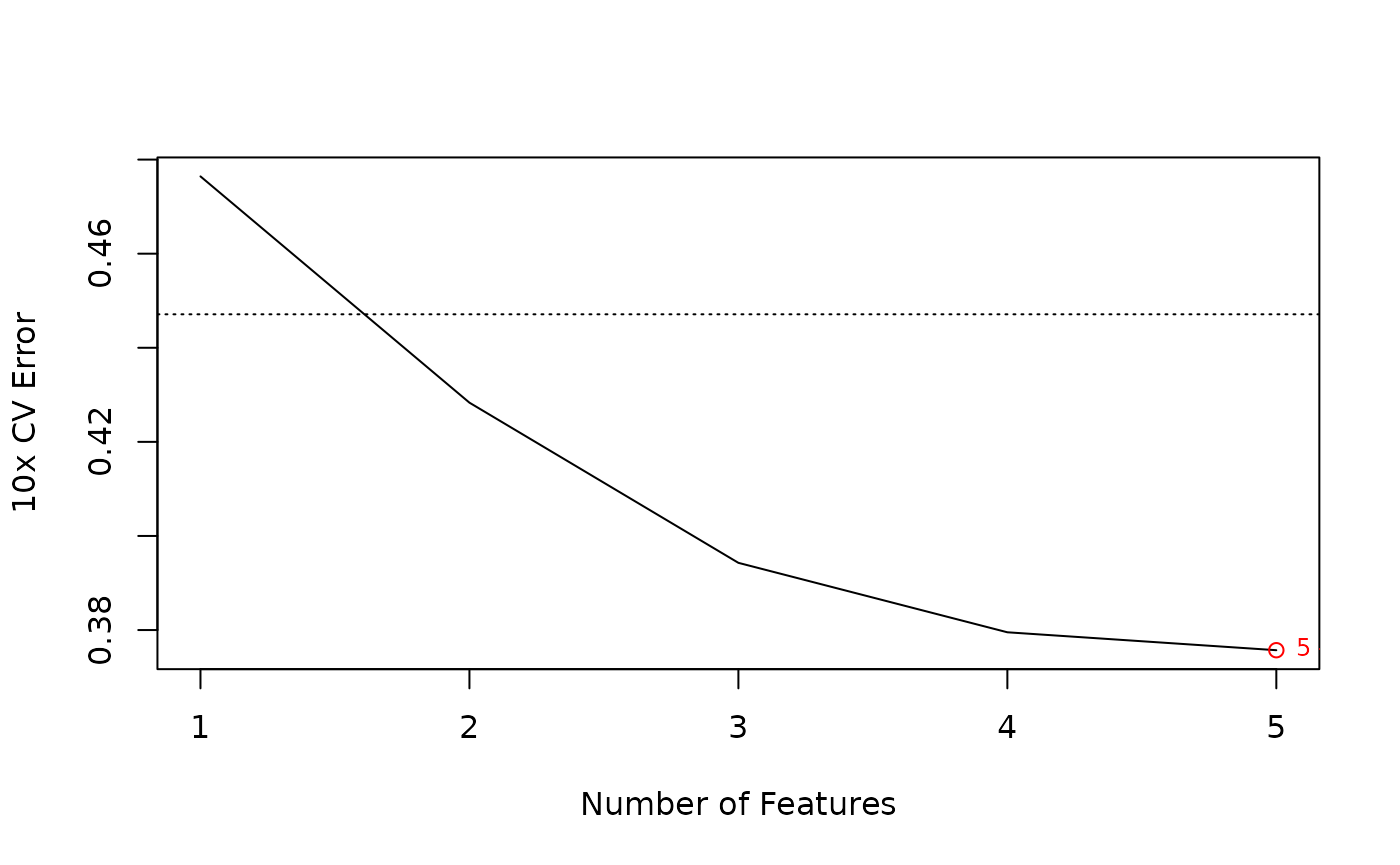
Parallelization
As you can probably see, the main limitation in doing this type of exploration is processing time. For example, in this demonstration, and just considering the number of times we have to fit an SVM, we have:
-
Feature ranking
10 external folds x 546 features x 10 msvmRFE folds = 54600 linear SVMs
-
Generalization error estimation
10 external folds x 546 features x 169 hyperparamter combos for exhaustive search x 10 folds each = 9227400 RBF kernel SVMs
We have already shortened this some by 1) eliminating more than one feature at a time in the feature ranking step, and 2) only estimating generalization accuracies across a sweep of the top features.
Other ideas to shorten processing time:
- Fewer external CV folds.
- Smaller or coarser grid for parameter sweep in SVM tuning step
- Fewer CV folds in SVM tuning step.
This code is already set up to use lapply calls for these 2 mains task, so fortunately, they can be relatively easily parallelized using a variety of R packages that include parallel versions of lapply. Examples include: